Local Search & Games

CSCI 4511/6511

Joe Goldfrank

Announcements

• Homework 1 is due on 15 September at 11:55 PM

  • Late submission policy

• Homework 2 is due on 29 September at 11:55 PM

• Fri 13 Sep Office Hours moved: 12 PM - 3 PM

• Fri 20 Sep Office Hours moved: 12 PM - 3 PM

Review

Why Are We Here?

Why Are We Here?

⠀⠀⠀⠀⠀⠀⠀⢀⣠⣤⣤⣶⣶⣶⣶⣤⣤⣄⡀⠀⠀⠀⠀⠀⠀⠀
⠀⠀⠀⠀⢀⣤⣾⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣷⣤⡀⠀⠀⠀⠀
⠀⠀⠀⣴⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡄⠀⠀⠀
⠀⢀⣾⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⠟⠁⠀⠀⠀
⠀⣾⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⠟⠋⠀⠀⠀⠀⠀⠀
⢠⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⠟⠋            ⠀⣀⣄⡀      ⠀⠀⣠⣄⡀
⢸⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣏⠀⠀⠀            ⢸⣿⣿⣿      ⠀⢸⣿⣿⣿
⠘⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣦⣀⠀            ⠉⠋⠁      ⠀⠀⠙⠋⠁
⠀⢿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣷⣦⡀⠀⠀⠀⠀⠀⠀
⠀⠈⢿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣷⣤⠀⠀⠀⠀
⠀⠀⠀⠻⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⠃⠀⠀⠀
⠀⠀⠀⠀⠈⠛⢿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡿⠛⠁⠀⠀⠀⠀
⠀⠀⠀⠀⠀⠀⠀⠈⠙⠛⠛⠿⠿⠿⠿⠛⠛⠋⠁⠀⠀⠀⠀⠀⠀⠀

Search: Why?

• Fully-observed problem
• Deterministic actions and state
• Well-defined start and goal
  • “Well-defined”

Goal Tests

Goal Tests

Best-First Search

A* Search

• Include path-cost \(g(n)\)
  • \(f(n) = g(n) + h(n)\)

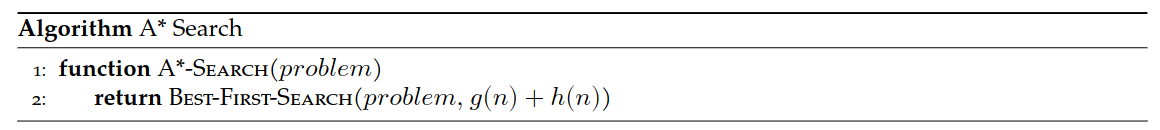
• Complete (always)
• Optimal (sometimes)
• Painful \(O(b^m)\) time and space complexity

A* vs. Dijkstra

Choosing Heuristics

• Recall: \(h(n)\) estimates cost from \(n\) to goal

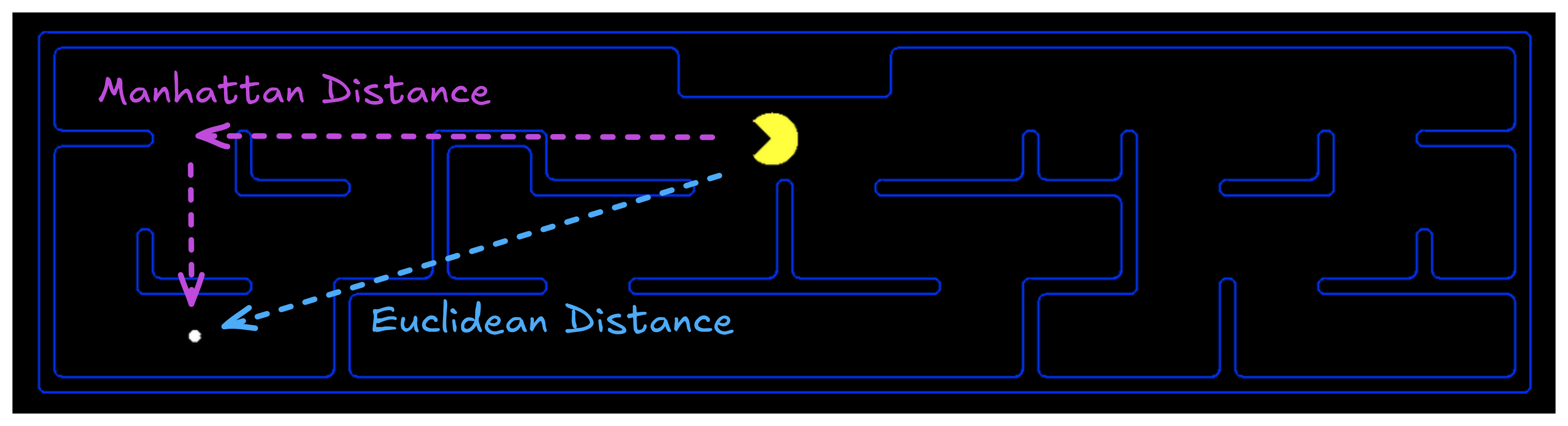
• Admissibility
• Consistency

Choosing Heuristics

• Admissibility
  • Never overestimates cost from \(n\) to goal
  • Cost-optimal!
• Consistency
  • \(h(n) \leq c(n, a, n') + h(n')\)
  • \(n'\) successors of \(n\)
  • \(c(n, a, n')\) cost from \(n\) to \(n'\) given action \(a\)

Iterative-Deepening A* Search

“IDA*” Search

• Similar to Iterative Deepening with Depth-First Search
  • DFS uses depth cutoff
  • IDA* uses \(h(n) + g(n)\) cutoff with DFS
  • Once cutoff breached, new cutoff:
    • Typically next-largest \(h(n) + g(n)\)
  • \(O(b^m)\) time complexity 😔
  • \(O(d)\) space complexity 😌

Beam Search

Best-First Search:

• Frontier is all expanded nodes

Beam Search:

• \(k\) “best” nodes are kept on frontier
  • Others discarded
• Alt: all nodes within \(\delta\) of best node
• Not Optimal
• Not Complete

Recursive Best-First Search (RBFS)

• No \(reached\) table is kept
• Second-best node \(f(n)\) retained
  • Search from each node cannot exceed this limit
  • If exceeded, recursion “backs up” to previous node
• Memory-efficient
  • Can “cycle” between branches

Recursive Best-First Search (RBFS)

Heuristic Characteristics

• What makes a “good” heuristic?
  • We know about admissability and consistency
  • What about performance?
• Effective branching factor
• Effective depth
• # of nodes expanded

Where Do Heuristics Come From?

• Intuition
  • “Just Be Really Smart”
• Relaxation
  • The problem is constrained
  • Remove the constraint
• Pre-computation
  • Sub problems
• Learning

Local Search

What Even Is The Goal?

Uninformed/Informed Search:

• Known start, known goal
• Search for optimal path

Local Search:

• “Start” is irrelevant
• Goal is not known
  • But we know it when we see it
• Search for goal

Brutal Example

Less-Brutal Example

“Real-World” Examples

• Scheduling
• Layout optimization
  • Factories
  • Circuits
• Portfolio management
• Others?

Objective Function

• Do you know what you want?¹
• Can you express it mathematically?²
  • A single value
  • More is better
• Objective function: a function of state

1. If not, you might be human

2. If not, you might be human

Hill-Climbing

• Objective function
• State space mapping
  • Neighbors

Hill-Climbing

The Hazards of Climbing Hills

• Local maxima
• Plateaus
• Ridges

Five Queens

Five Queens

Five Queens

Variations

• Sideways moves
  • Not free
• Stochastic moves
  • Full set
  • First choice
• Random restarts
  • If at first you don’t succeed, you fail try again!
  • Complete 😌

The Trouble with Local Maxima

• We don’t know that they’re local maxima
  • Unless we do?
• Hill climbing is efficient
  • But gets trapped
• Exhaustive search is complete
  • But it’s exhaustive!
  • Stochastic methods are ‘exhaustive’

Simulated Annealing

Simulated Annealing

• Doesn’t actually have anything to do with metallurgy
• Search begins with high “temperature”
  • Temperature decreases during search
• Next state selected randomly
  • Improvements always accepted
  • Non-improvements rejected stochastically
  • Higher temperature, less rejection
  • “Worse” result, more rejection

Simulated Annealing

Local Beam Search

Recall:

• Beam search keeps track of \(k\) “best” branches

Local Beam Search:

• Hill climbing search, keeping track of \(k\) successors
  • Deterministic
  • Stochastic

Local Beam Search

The Real World Is Discrete

(it isn’t)

The Real World Is Not Discrete

• Discretize continuous space
  • Works iff no objective function discontinuities
  • What happens if there are discontinuities?
  • How do we know that there are discontinuities?

Gradient Descent

• Minimize loss instead of climb hill
  • Still the same idea

Consider:

• One state variable, \(x\)
• Objective function \(f(x)\)
  • How do we minimize \(f(x)\) ?
  • Is there a closed form \(\frac{d}{dx}\) ?

Gradient Descent

Multivariate \(\vec{x} = x_0, x_1, ...\)

Instead of derivative, gradient:

\(\nabla f(\vec{x}) = \left[ \frac{\partial f}{\partial x_0}, \frac{\partial f}{\partial x_1}, ...\right]\)

“Locally” descend gradient:

\(\vec{x} \gets \vec{x} + \alpha \nabla f(\vec{x})\)

Games

Adversity

So far:

• The world does not care about us
• This is a simplifying assumption!

Reality:

• The world does not care us

• …but it wants things for “itself”

• …and we don’t want the same things

The Adversary

One extreme:

• Single adversary
  • Adversary wants the exact opposite from us
  • If adversary “wins,” we lose

😐

Other extreme:

• An entire world of agents with different values
  • They might want some things similar to us
• “Economics”

😐

Simple Games

• Two-player
• Turn-taking
• Discrete-state
• Fully-observable
• Zero-sum
  • This does some work for us!

Max and Min

• Two players want the opposite of each other
• State takes into account both agents
  • Actions depend on whose turn it is

Minimax

• Initial state \(s_0\)
• Actions(\(s\)) and To-move(\(s\))
• Result(\(s, a\))
• Is-Terminal(\(s\))
• Utility(\(s, p\))

Minimax

Minimax

More Than Two Players

• Two players, two values: \(v_A, v_B\)
  • Zero-sum: \(v_A = -v_B\)
  • Only one value needs to be explicitly represented
• \(> 2\) players:
  • \(v_A, v_B, v_C ...\)
  • Value scalar becomes \(\vec{v}\)

Society

• \(>2\) players, only one can win
• Cooperation can be rational!

Example:

• A & B: 30% win probability each
• C: 40% win probability
• A & B cooperate to eliminate C
  • \(\rightarrow\) A & B: 50% win probability each

…what about friendship?

Minimax Efficiency

Pruning removes the need to explore the full tree.

• Max and Min nodes alternate
• Once one value has been found, we can eliminate parts of search
  • Lower values, for Max
  • Higher values, for Min
• Remember highest value (\(\alpha\)) for Max
• Remember lowest value (\(\beta\)) for Min

Pruning

Heuristics 😌

• In practice, trees are far too deep to completely search
• Heuristic: replace utility with evaluation function
  • Better than losing, worse than winning
  • Represents chance of winning
• Chance? 🎲🎲
  • Even in deterministic games
  • Why?

More Pruning

• Don’t bother further searching bad moves
  • Examples?
• Beam search
  • Lee Sedol’s singular win against AlphaGo

Other Techniques

• Move ordering
  • How do we decide?
• Lookup tables
  • For subsets of games

Monte Carlo Tree Search

• Many games are too large even for an efficient \(\alpha\)-\(\beta\) search 😔
  • We can still play them
• Simulate plays of entire games from starting state
  • Update win probability from each node (for each player) based on result
• “Explore/exploit” paradigm for move selection

Choosing Moves

• We want our search to pick good moves
• We want our search to pick unknown moves
• We don’t want our search to pick bad moves
  • (Assuming they’re actually bad moves)

Select moves based on a heuristic.

Games of Luck

• Real-world problems are rarely deterministic
• Non-deterministic state evolution:
  • Roll a die to determine next position
  • Toss a coin to determine who picks candy first
  • Precise trajectory of kicked football¹
  • Others?

1. Any definition of “football”

Solving Non-Deterministic Games

Previously: Max and Min alternate turns

Now:

• Max
• Chance
• Min
• Chance

😣

Expectiminimax

• “Expected value” of next position

• How does this impact branching factor of the search?

🫠

Expectiminimax

Filled With Uncertainty

What is to be done?

• Pruning is still possible
  • How?
• Heuristic evaluation functions
  • Choose carefully!

Non-Optimal Adversaries

• Is deterministic “best” behavior optimal?
• Are all adversaries rational?

• Expectimax

References

• Stuart J. Russell and Peter Norvig. Artificial Intelligence: A Modern Approach. 4th Edition, 2020.

• Mykal Kochenderfer, Tim Wheeler, and Kyle Wray. Algorithms for Decision Making. 1st Edition, 2022.

• Stanford CS231

• Stanford CS228

• UC Berkeley CS188