Constraint Satisfaction
CSCI 4511/6511
Announcements
Homework 2 is due on 29 September at 11:55 PM
Fri 20 Sep Office Hours moved: 12 PM - 3 PM
Autograder
![]()
Review and Saved Rounds
Simple Games
- Two-player
- Turn-taking
- Discrete-state
- Fully-observable
- Zero-sum
- This does some work for us!
Max and Min
- Two players want the opposite of each other
- State takes into account both agents
- Actions depend on whose turn it is
Minimax
- Initial state \(s_0\)
- Actions(\(s\)) and To-move(\(s\))
- Result(\(s, a\))
- Is-Terminal(\(s\))
- Utility(\(s, p\))
Minimax
Minimax

More Than Two Players
- Two players, two values: \(v_A, v_B\)
- Zero-sum: \(v_A = -v_B\)
- Only one value needs to be explicitly represented
- \(> 2\) players:
- \(v_A, v_B, v_C ...\)
- Value scalar becomes \(\vec{v}\)
Minimax Efficiency
Pruning removes the need to explore the full tree.
- Max and Min nodes alternate
- Once one value has been found, we can eliminate parts of search
- Lower values, for Max
- Higher values, for Min
- Remember highest value (\(\alpha\)) for Max
- Remember lowest value (\(\beta\)) for Min
Pruning
Heuristics 😌
- In practice, trees are far too deep to completely search
- Heuristic: replace utility with evaluation function
- Better than losing, worse than winning
- Represents chance of winning
- Chance? 🎲🎲
- Even in deterministic games
- Why?
More Pruning
- Don’t bother further searching bad moves
- Examples?
- Beam search
- Lee Sedol’s singular win against AlphaGo
Heuristic + Cutoff
Other Techniques
- Move ordering
- How do we decide?
- Lookup tables
- For subsets of games
Monte Carlo Tree Search
- Many games are too large even for an efficient \(\alpha\)-\(\beta\) search 😔
- We can still play them
- Simulate plays of entire games from starting state
- Update win probability from each node (for each player) based on result
- “Explore/exploit” paradigm for move selection
Choosing Moves
- We want our search to pick good moves
- We want our search to pick unknown moves
- We don’t want our search to pick bad moves
- (Assuming they’re actually bad moves)
Select moves based on a heuristic.
Games of Luck
- Real-world problems are rarely deterministic
- Non-deterministic state evolution:
- Roll a die to determine next position
- Toss a coin to determine who picks candy first
- Precise trajectory of kicked football1
- Others?
Solving Non-Deterministic Games
Previously: Max and Min alternate turns
Now:
- Max
- Chance
- Min
- Chance
😣
Expectiminimax
- “Expected value” of next position

- How does this impact branching factor of the search?
🫠
Expectiminimax
Filled With Uncertainty
What is to be done?
- Pruning is still possible
- How?
- Heuristic evaluation functions
- Choose carefully!
Non-Optimal Adversaries
- Is deterministic “best” behavior optimal?
- Are all adversaries rational?
- Expectimax
CSPs
Factored Representation
- Encode relationships between variables and states
- Solve problems with general search algorithms
- Heuristics do not require expert knowledge of problem
- Encoding problem requires expert knowledge of problem1
Why?
Constraint Satisfaction
- Express problem in terms of state variables
- Constrain state variables
- Begin with all variables unassigned
- Progressively assign values to variables
- Assignment of values to state variables that “works:” solution
More Formally
- State variables: \(X_1, X_2, ... , X_n\)
- State variable domains: \(D_1, D_2, ..., D_n\)
- The domain specifies which values are permitted for the state variable
- Domain: set of allowable variables (or permissible range for continuous variables)1
- Some constraints \(C_1, C_2, ..., C_m\) restrict allowable values
Constraint Types
- Unary: restrict single variable
- Can be rolled into domain
- Why even have them?
- Binary: restricts two variables
- Global: restrict “all” variables
Constraint Examples
- \(X_1\) and \(X_2\) both have real domains, i.e. \(X_1, X_2 \in \mathbb{R}\)
- A constraint could be \(X_1 < X_2\)
- \(X_1\) could have domain \(\{\text{red}, \text{green}, \text{blue}\}\) and \(X_2\) could have domain \(\{\text{green}, \text{blue}, \text{orange}\}\)
- A constraint could be \(X_1 \neq X_2\)
- \(X_1, X_2, ..., X_100 \in \mathbb{R}\)
- Constraint: exactly four of \(X_i\) equal 12
- Rewrite as binary constraint?
Assignments
- Assignments must be to values in each variable’s domain
- Assignment violates constraints?
- Consistency
- All variables assigned?
- Complete
Yugoslavia1
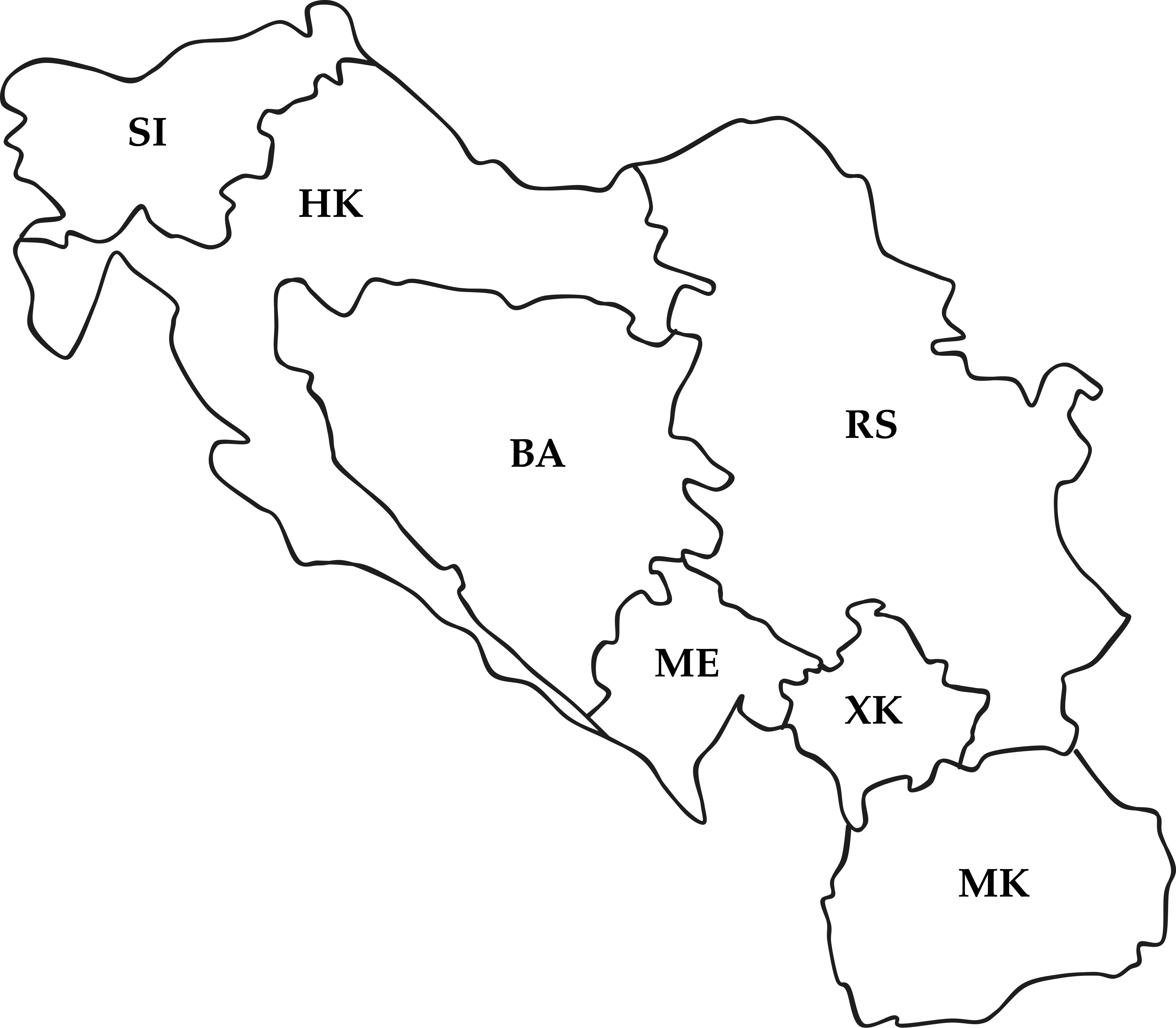
Four-Colorings
Two possibilities:
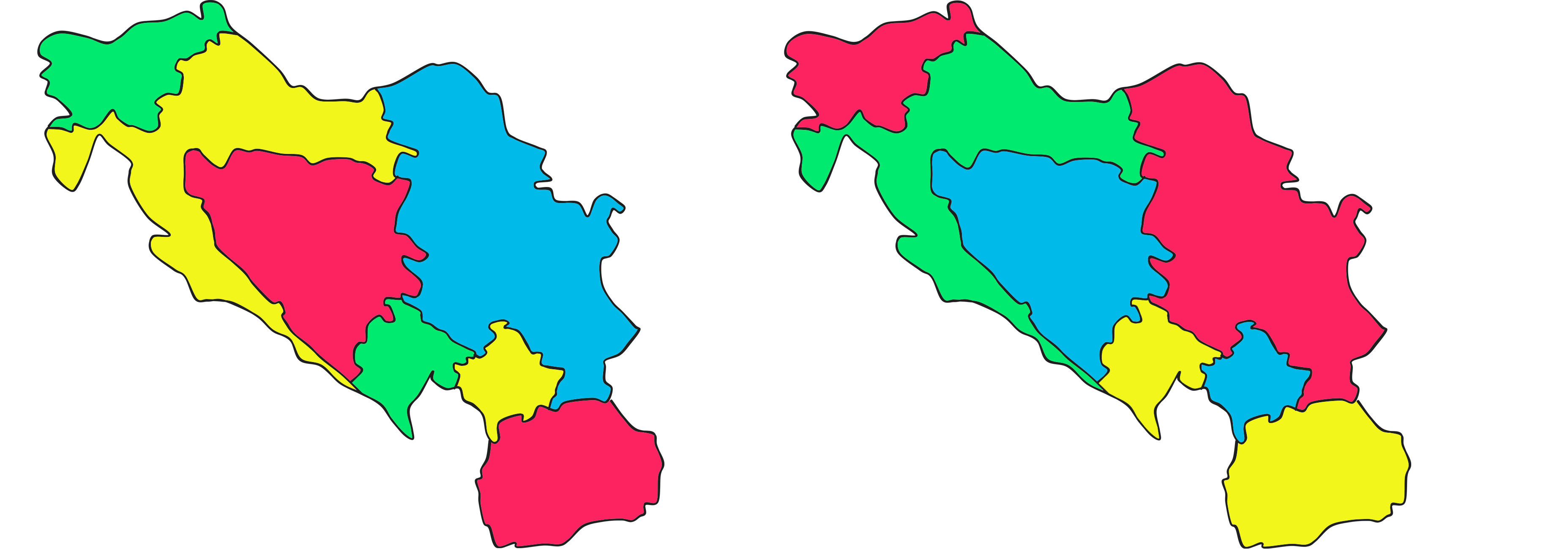
Formulate as CSP?

Graph Representations
- Constraint graph:
- Nodes are variables
- Edges are constraints
- Constraint hypergraph:
- Variables are nodes
- Constraints are nodes
- Edges show relationship
Why have two different representations?
Graph Representation I
Constraint graph: edges are constraints

Graph Representation II
Constraint hypergraph: constraints are nodes

How To Solve It
- We can search!
- …the space of consistent assignments
- Complexity \(O(d^n)\)
- Domain size \(d\), number of nodes \(n\)
- Tree search for node assignment
- Inference to reduce domain size
- Recursive search
How To Solve It
What Even Is Inference
- Constraints on one variable restrict others:
- \(X_1 \in \{A, B, C, D\}\) and \(X_2 \in \{A\}\)
- \(X_1 \neq X_2\)
- Inference: \(X_1 \in \{B, C, D\}\)
- If an unassigned variable has no domain…
- Failure
Inference
- Arc consistency
- Reduce domains for pairs of variables
- Path consistency
- Assignment to two variables
- Reduce domain of third variable
AC-3

How To Solve It (Again)
Backtracking search:
- Similar to DFS
- Variables are ordered
- Why?
- Constraints checked each step
- Constraints optionally propagated
How To Solve It (Again)
Yugoslav Arc Consistency

Ordering
- Select-Unassgined-Variable(\(CSP, assignment\))
- Choose most-constrained variable1
- Order-Domain-Variables(\(CSP, var, assignment\))
- Least-constraining value
- Why?
Restructuring
Tree-structured CSPs:
Linear time solution
Directional arc consistency: \(X_i \rightarrow X_{i+1}\)
Cutsets
Sub-problems
Cutset Example

(Heuristic) Local Search
- Hill climbing
- Random restarts
- Simulated annealing
- Fast?
- Complete?
- Optimal?
Continuous Domains
- Linear:
\[\begin{aligned} \max_{x} \quad & \boldsymbol{c}^T\boldsymbol{x}\\ \textrm{s.t.} \quad & A\boldsymbol{x} \leq \boldsymbol{b}\\ &\boldsymbol{x} \geq 0 \\ \end{aligned}\]
- Convex
\[\begin{aligned} \min_{x} \quad & f(\boldsymbol{x})\\ \textrm{s.t.} \quad & g_i(\boldsymbol{x}) \leq 0\\ & h_i(\boldsymbol{x}) = 0 \\ \end{aligned}\]

Is This Even Relevant in 2024?
- Absolutely yes.
- LLMs are bad at CSPs
- CSPs are common in the real world
- Scheduling
- Optimization
- Dependency solvers
Logic Preview
\(R_{HK} \Rightarrow \neg R_{SI}\)
\(G_{HK} \Rightarrow \neg G_{SI}\)
\(B_{HK} \Rightarrow \neg B_{SI}\)
\(R_{HK} \lor G_{HK} \lor B_{HK}\)
…
Goal: find assignment of variables that satisifies conditions
References
Stuart J. Russell and Peter Norvig. Artificial Intelligence: A Modern Approach. 4th Edition, 2020.
Mykal Kochenderfer, Tim Wheeler, and Kyle Wray. Algorithms for Decision Making. 1st Edition, 2022.
Stanford CS231
Stanford CS228
UC Berkeley CS188