Midterm Review

CSCI 4511/6511

Joe Goldfrank

Announcements

• Midterm Exam - 16 Oct
  • In class
  • Open note: 10 sides of paper (8.5”x11” or A4)
• Homework Three - 20 Oct
• Project Guidelines

Review

The Rational Agent

• Has a utility function
  • Maximizes expected utility
• Sensors: perceives environment
• Actuators: influences environment

What is in between sensors and actuators?

The agent function.

Reflex Agent

• Very basic form of agent function
• Percept \(\rightarrow\) Action lookup table
• Good for simple games
  • Tic-tac-toe
  • Checkers?
• Needs entire state space in table

State Space Size

• Tic-tac-toe: \(10^3\)
• Checkers: \(10^{20}\)
• Chess: \(10^{44}\)
• Go: \(10^{170}\)
• Self-driving car: ?
• Pacman?
  • How could you estimate it?

In Practice

• Environment
  • What happens next
• Perception
  • What agent can see
• Action
  • What agent can do
• Measure/Reward
  • Encoded utility function

Search

• Fully-observed problem
• Deterministic actions and state
• Well defined start and goal

Not Search

• Uncertainty
  • State transitions known
• Adversary
  • Nobody wants us to lose
• Cooperation
• Continuous state

Search Problem

Search problem includes:

• Start State
• State Space
• State Transitions
• Goal Test

State Space:

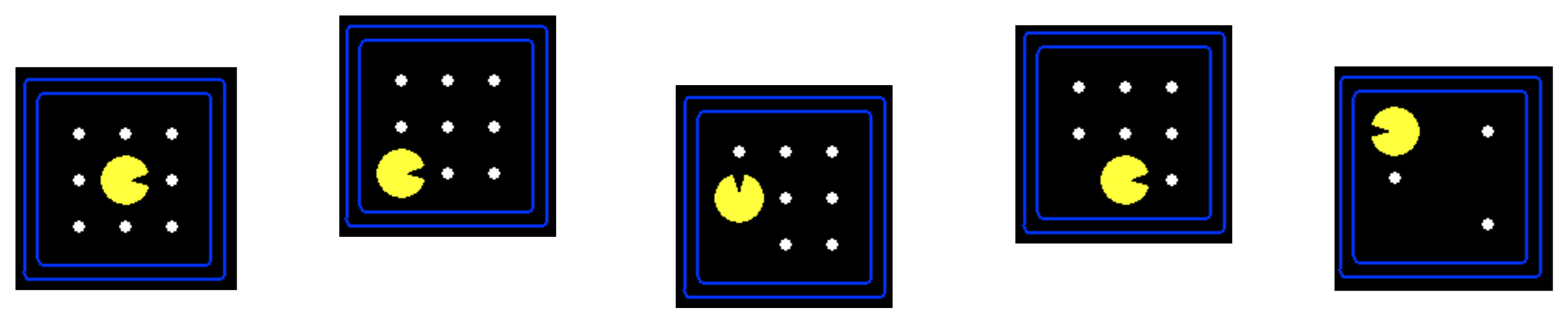
Actions & Successor States:

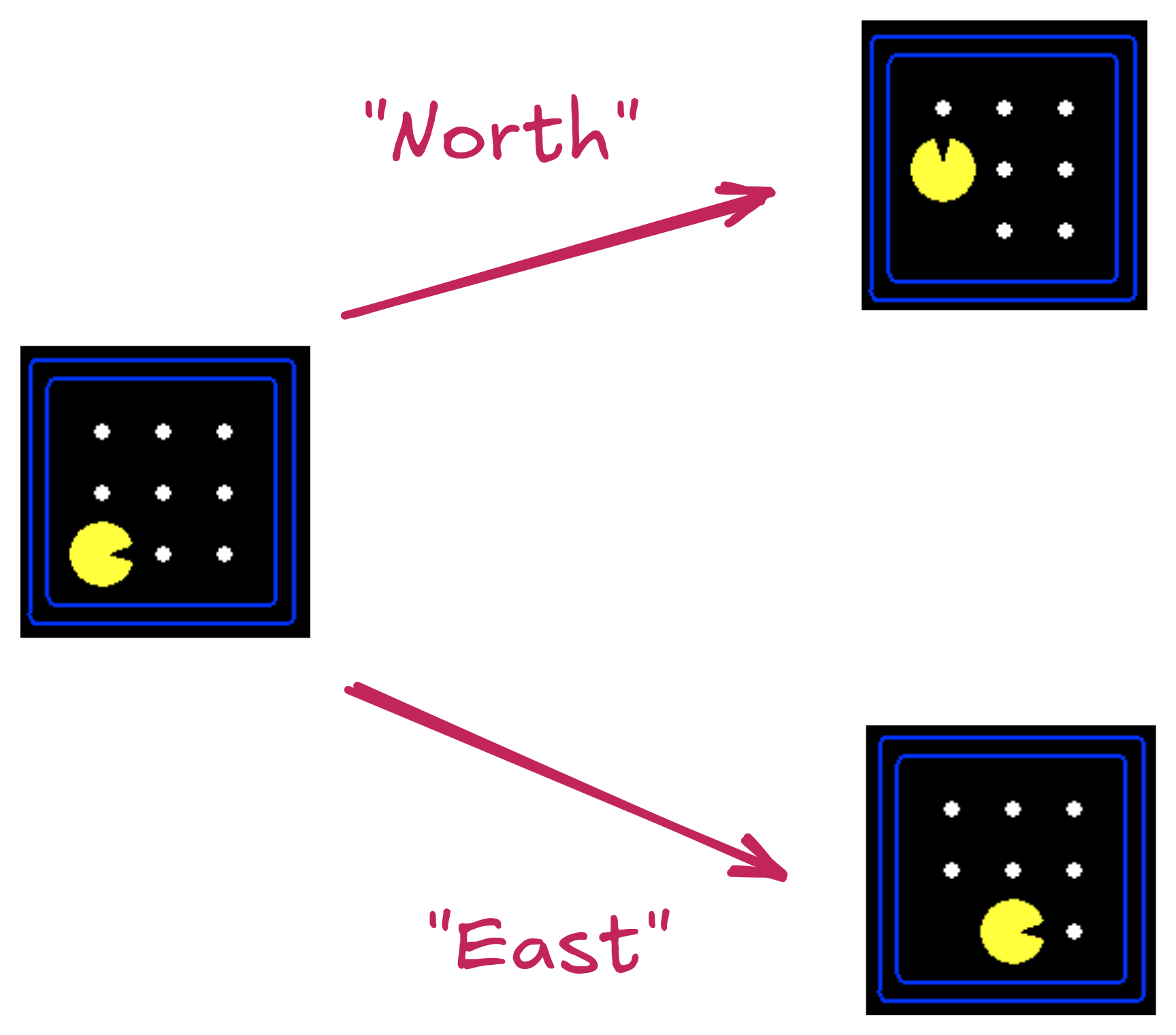
State Space

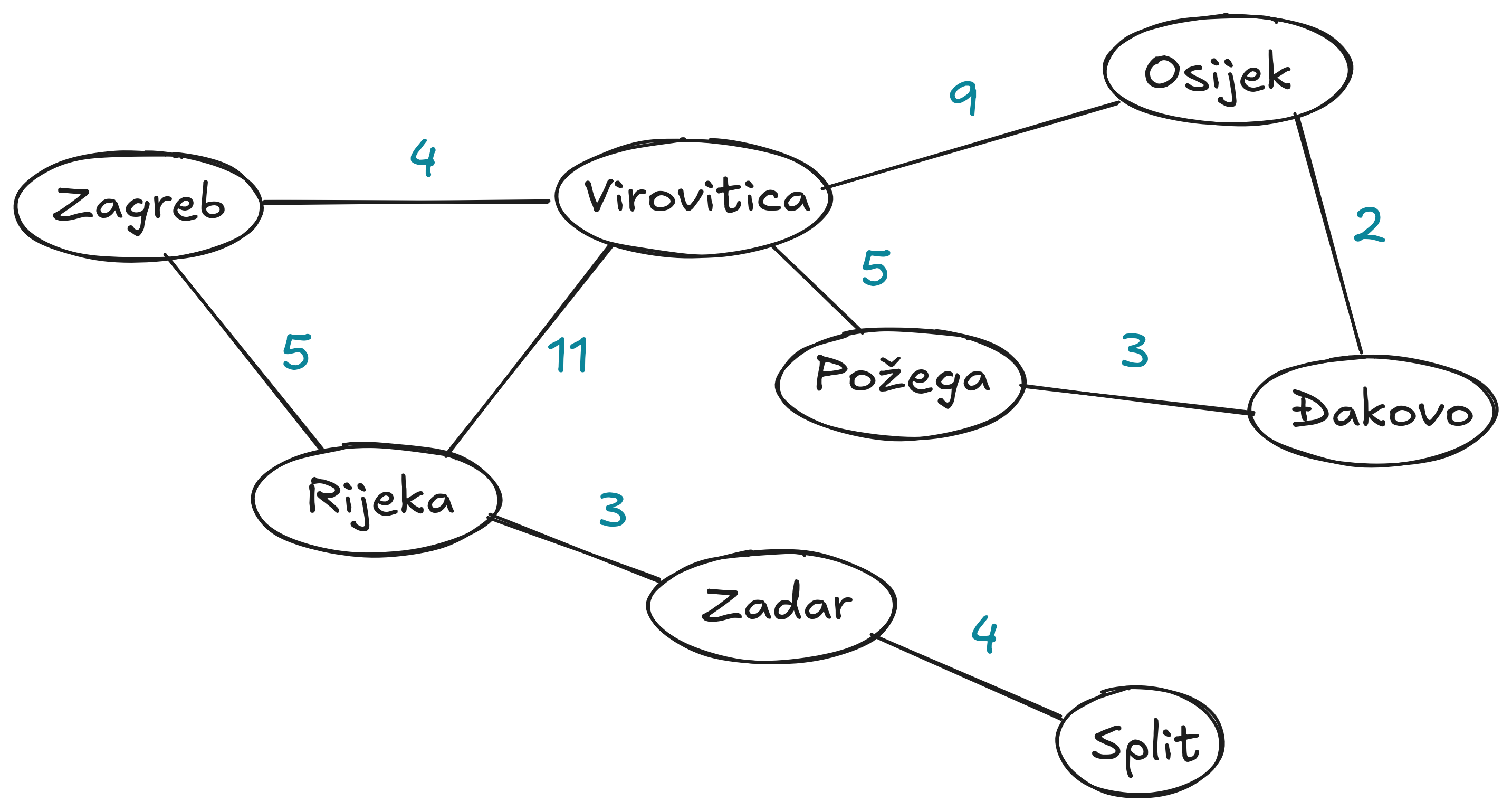
State Space Graph

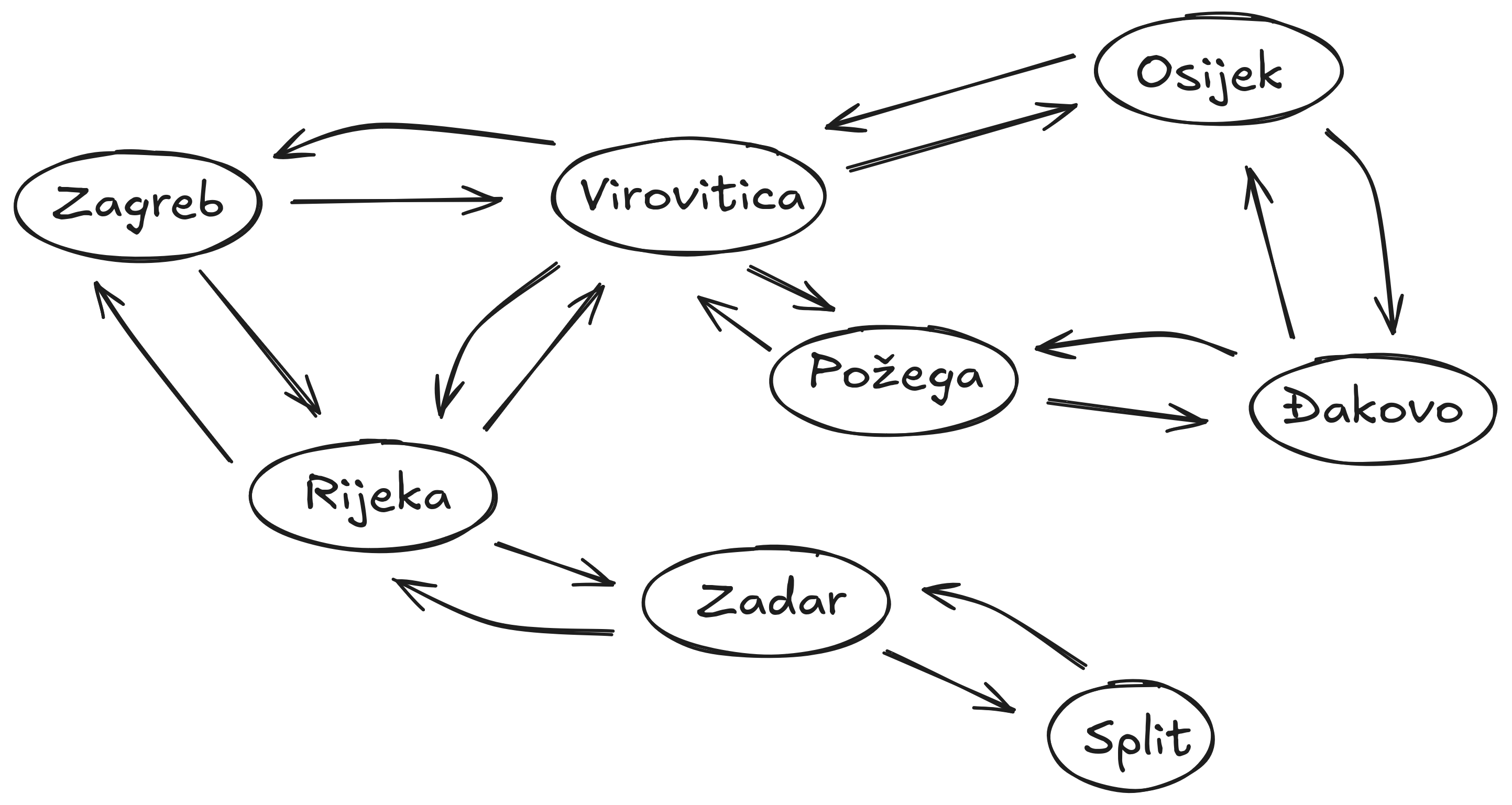
Graph vs. Tree

How To Solve It

Given:

• Starting node
• Goal test
• Expansion

Do:

• Expand nodes from start
• Test each new node for goal
  • If goal, success
• Expand new nodes
  • If nothing left to expand, failure

Queues & Searches

• Priority Queues
  • Best-First Search
  • Uniform-Cost Search¹
• FIFO Queues
  • Breadth-First Search
• LIFO Queues²
  • Depth-First Search

1. Also known as “Dijkstra’s Algorithm,” because it is Dijkstra’s Algorithm

2. Also known as “stacks,” because they are stacks.

Search Features

• Completeness
  • If there is a solution, will we find it?
• Optimality
  • Will we find the best solution?
• Time complexity
• Memory complexity

Uninformed Search Variants

• Depth-Limited Search
  • Fail if depth limit reached (why?)
• Iterative deepening
  • vs. Breadth-First Search
• Bidirectional Search

Heuristics

heuristic - adj - Serving to discover or find out.¹

• We know things about the problem
• These things are external to the graph/tree structure
  • We could model the problem differently
  • We can use the information directly

1. Webster’s, 1913

Choosing Heuristics

• Admissibility
  • Never overestimates cost from \(n\) to goal
  • Cost-optimal!
• Consistency
  • \(h(n) \leq c(n, a, n') + h(n')\)
  • \(n'\) successors of \(n\)
  • \(c(n, a, n')\) cost from \(n\) to \(n'\) given action \(a\)

Weighted A* Search

• Greedy: \(f(n) = h(n)\)
• A*: \(f(n) = h(n) + g(n)\)
• Uniform-Cost Search: \(f(n) = g(n)\)

• Weighted A* Search: \(f(n) = W\cdot h(n) + g(n)\)
  • Weight \(W > 1\)

Iterative-Deepening A* Search

“IDA*” Search

• Similar to Iterative Deepening with Depth-First Search
  • DFS uses depth cutoff
  • IDA* uses \(h(n) + g(n)\) cutoff with DFS
  • Once cutoff breached, new cutoff:
    • Typically next-largest \(h(n) + g(n)\)
  • \(O(b^m)\) time complexity 😔
  • \(O(d)\) space complexity¹ 😌

1. This is slightly complicated based on heuristic branching factor \(b_h\).

Beam Search

Best-First Search:

• Frontier is all expanded nodes

Beam Search:

• \(k\) “best” nodes are kept on frontier
  • Others discarded
• Alt: all nodes within \(\delta\) of best node
• Not Optimal
• Not Complete

Where Do Heuristics Come From?

• Intuition
  • “Just Be Really Smart”
• Relaxation
  • The problem is constrained
  • Remove the constraint
• Pre-computation
  • Sub problems
• Learning

Local Search

Uninformed/Informed Search:

• Known start, known goal
• Search for optimal path

Local Search:

• “Start” is irrelevant
• Goal is not known
  • But we know it when we see it
• Search for goal

Objective Function

• Do you know what you want?
• Can you express it mathematically?
  • A single value
  • More is better
• Objective function: a function of state

Hill-Climbing

• Objective function
• State space mapping
  • Neighbors

Hazards:

• Local maxima
• Plateaus
• Ridges

Variations

• Sideways moves
  • Not free
• Stochastic moves
  • Full set
  • First choice
• Random restarts
  • If at first you don’t succeed, you fail try again!
  • Complete 😌

Simulated Annealing

• Search begins with high “temperature”
  • Temperature decreases during search
• Next state selected randomly
  • Improvements always accepted
  • Non-improvements rejected stochastically
  • Higher temperature, less rejection
  • “Worse” result, more rejection

Local Beam Search

Recall:

• Beam search keeps track of \(k\) “best” branches

Local Beam Search:

• Hill climbing search, keeping track of \(k\) successors
  • Deterministic
  • Stochastic

Gradient Descent

• Minimize loss instead of climb hill
  • Still the same idea

Consider:

• One state variable, \(x\)
• Objective function \(f(x)\)
  • How do we minimize \(f(x)\) ?
  • Is there a closed form \(\frac{d}{dx}\) ?

Gradient Descent

Multivariate \(\vec{x} = x_0, x_1, ...\)

Instead of derivative, gradient:

\(\nabla f(\vec{x}) = \left[ \frac{\partial f}{\partial x_0}, \frac{\partial f}{\partial x_1}, ...\right]\)

“Locally” descend gradient:

\(\vec{x} \gets \vec{x} + \alpha \nabla f(\vec{x})\)

I will not ask you to take a derivative on the exam.

Adversity

So far:

• The world does not care about us
• This is a simplifying assumption!

Reality:

• The world does not care us

• It wants things for “itself”

• We don’t want the same things

The Adversary

One extreme:

• Single adversary
  • Adversary wants the exact opposite from us
  • If adversary “wins,” we lose 😐

Other extreme:

• An entire world of agents with different values
  • They might want some things similar to us
• “Economics” 😐

Simple Games: Max and Min

• Two players want the opposite of each other
• State takes into account both agents
  • Actions depend on whose turn it is

Minimax

• Initial state \(s_0\)
• Actions(\(s\)) and To-move(\(s\))
• Result(\(s, a\))
• Is-Terminal(\(s\))
• Utility(\(s, p\))

More Than Two Players

• Two players, two values: \(v_A, v_B\)
  • Zero-sum: \(v_A = -v_B\)
  • Only one value needs to be explicitly represented
• \(> 2\) players:
  • \(v_A, v_B, v_C ...\)
  • Value scalar becomes \(\vec{v}\)

Minimax Efficiency

Pruning removes the need to explore the full tree.

• Max and Min nodes alternate
• Once one value has been found, we can eliminate parts of search
  • Lower values, for Max
  • Higher values, for Min
• Remember highest value (\(\alpha\)) for Max
• Remember lowest value (\(\beta\)) for Min

Heuristics 😌

• In practice, trees are far too deep to completely search
• Heuristic: replace utility with evaluation function
  • Better than losing, worse than winning
  • Represents chance of winning
• Chance? 🎲🎲
  • Even in deterministic games
  • Why?

Solving Non-Deterministic Games

Previously: Max and Min alternate turns

Now:

• Max
• Chance
• Min
• Chance

Constraint Satisfaction

• Express problem in terms of state variables
  • Constrain state variables
• Begin with all variables unassigned
• Progressively assign values to variables
• Assignment of values to state variables that “works:” solution

More Formally

• State variables: \(X_1, X_2, ... , X_n\)
• State variable domains: \(D_1, D_2, ..., D_n\)
  • The domain specifies which values are permitted for the state variable
  • Domain: set of allowable variables (or permissible range for continuous variables)¹
  • Some constraints \(C_1, C_2, ..., C_m\) restrict allowable values

1. Or a hybrid, such as a union of ranges of continuous variables.

Constraint Types

• Unary: restrict single variable
  • Can be rolled into domain
  • Why even have them?
• Binary: restricts two variables
• Global: restrict “all” variables

Assignments

• Assignments must be to values in each variable’s domain
• Assignment violates constraints?
  • Consistency
• All variables assigned?
  • Complete

Four-Colorings

Two possibilities:

Graph Representations

• Constraint graph:
  • Nodes are variables
  • Edges are constraints
• Constraint hypergraph:
  • Variables are nodes
  • Constraints are nodes
  • Edges show relationship

Why have two different representations?

Graph Representation I

Constraint graph: edges are constraints

Graph Representation II

Constraint hypergraph: constraints are nodes

Inference

• Constraints on one variable restrict others:
  • \(X_1 \in \{A, B, C, D\}\) and \(X_2 \in \{A\}\)
  • \(X_1 \neq X_2\)
  • Inference: \(X_1 \in \{B, C, D\}\)
• If an unassigned variable has no domain…
  • Failure

Inference

• Arc consistency
  • Reduce domains for pairs of variables
• Path consistency
  • Assignment to two variables
  • Reduce domain of third variable

Ordering

• Select-Unassgined-Variable(\(CSP, assignment\))
  • Choose most-constrained variable¹
• Order-Domain-Variables(\(CSP, var, assignment\))
  • Least-constraining value
• Why?

1. or MRV: “Minimum Remaining Values”

Restructuring

Tree-structured CSPs:

• Linear time solution

• Directional arc consistency: \(X_i \rightarrow X_{i+1}\)

• Topological sort complexity

  • Nothing is free

Logic

• Propositional symbols
  • Similar to boolean variables
  • Either True or False
  • Represent something in “real world”

Sentences

• What is a linguistic sentence?
  • Subject(s)
  • Verb(s)
  • Object(s)
  • Relationships
• What is a logical sentence?
  • Symbols
  • Relationships

Familiar Logical Operators

• \(\neg\)
  • “Not” operator, same as CS (!, not, etc.)
• \(\land\)
  • “And” operator, same as CS (&&, and, etc.)
  • This is sometimes called a conjunction.
• \(\lor\)
  • “Inclusive Or” operator, same as CS.
  • This is sometimes called a disjunction.

Unfamiliar Logical Operators

• \(\Rightarrow\)
  • Logical implication.
    
  • If \(X_0 \Rightarrow X_1\), \(X_1\) is always True when \(X_0\) is True.
    
  • If \(X_0\) is False, the value of \(X_1\) is not constrained.
• \(\iff\)
  • “If and only If.”
  • If \(X_0 \iff X_1\), \(X_0\) and \(X_1\) are either both True or both False.
  • Also called a biconditional.

Equivalent Statements

• \(X_0 \Rightarrow X_1\) alternatively:
  • \((X_0 \land X_1) \lor \neg X_0\)
• \(X_0 \iff X_1\) alternatively:
  • \((X_0 \land X_1) \lor (\neg X_0 \land \neg X_1)\)

Entailment

• \(KB \models A\)
  • “Knowledge Base entails A”
  • For every model in which \(KB\) is True, \(A\) is also True
  • One-way relationship: \(A\) can be True for models where \(KB\) is not True.
• Vocabulary: \(A\) is the query

Knowing Things

Falsehood:

• \(KB \models \neg A\)
  • No model exists where \(KB\) is True and \(A\) is True

It is possible to not know things:¹

• \(KB \nvdash A\)
• \(KB \nvdash \neg A\)

1. \(\nvdash\) – “does not entail”

Satisfiability

• Commonly abbreviated “SAT”

• First NP-complete problem

• \((X_0 \land X_1) \lor X_2\)

  • Satisfied by \(X_0 = \text{True}, X_1 = \text{False}, X_2 = \text{True}\)
  • Satisfied for any \(X_0\) and \(X_1\) if \(X_2 = \text{True}\)

• \(X_0 \land \neg X_0 \land X_1\)

  • Cannot be satisfied by any values of \(X_0\) and \(X_1\)

Conjunctive Normal Form

• Literals — symbols or negated symbols
  • \(X_0\) is a literal
  • \(\neg X_0\) is a literal
• Clauses — combine literals and disjunction using disjunctions (\(\lor\))
  • \(X_0 \lor \neg X_1\) is a valid disjunction
  • \((X_0 \lor \neg X_1) \lor X_2\) is a valid disjunction

Conjunctive Normal Form

• Conjunctions (\(\land\)) combine clauses (and literals)
  • \(X_1 \land (X_0 \lor \neg X_2)\)
• Disjunctions cannot contain conjunctions:
• \(X_0 \lor (X_1 \land X_2)\) not in CNF
  • Can be rewritten in CNF: \((X_0 \lor X_1) \land (X_0 \lor X_2)\)

Converting to CNF

• \(X_0 \iff X_1\)
  • \((X_0 \Rightarrow X_1) \land (X_1 \Rightarrow X_0)\)
• \(X_0 \Rightarrow X_1\)
  • \(\neg X_0 \lor X_1\)
• \(\neg (X_0 \land X_1)\)
  • \(\neg X_0 \lor \neg X_1\)
• \(\neg (X_0 \lor X_1)\)
  • \(\neg X_0 \land \neg X_1\)

Probability

• Not on exam

😌

• Very important, however
• Basis for remainder of course
• Sorry.

Bayesian Networks

References

• Stuart J. Russell and Peter Norvig. Artificial Intelligence: A Modern Approach. 4th Edition, 2020.

• Mykal Kochenderfer, Tim Wheeler, and Kyle Wray. Algorithms for Decision Making. 1st Edition, 2022.

• Stanford CS231

• UC Berkeley CS188